FORZA ELASTICA

Ho spiegato ciò che stai cercando in un video. Non ti dimenticare di iscriverti al canale e lasciare like!

Buona visione!

Se invece ti trovi meglio a leggere ecco tutto ciò che devi sapere sulla Forza Elastica.

FORZA ELASTICA:

Per definire cosa è la forza elastica, iniziamo da un esempio.

Prendiamo una molla attaccata ad un muro e poggiata su una superfice.

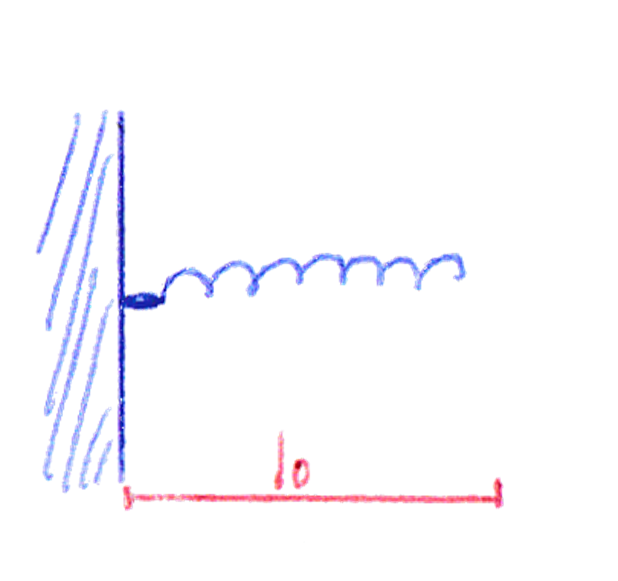
In questa figura abbiamo la lunghezza della molla a riposo che chiamiamo l0.

Se iniziamo ad allungare la forza verso destra, si otterrà un'altra lunghezza che chiamiamo l1.

Prendiamo come sistema di riferimento l'asse x con origine sull'origine della molla. Possiamo trovare Δl (la differenza di allungamento).

La formula per ottenere la differenza di allungamento sarà Δl = l1 - l0

La Forza Elastica è la forza che si oppone all’ allungamento o alla compressione da parte di una forza, per far ritornare alla lunghezza di riposo la molla.

La forza elastica è anche detta Legge di Hooke. Robert Hooke formulò questa legge nel 1675 e l’ equazione che esprime la forza elastica esercitata da una molla è:

F = - k ∙ x ∙ ux

x = Δl. Spostamento dalla posizione di equilibrio (positivo se la molla si allunga verso destra, negativo se si comprime verso sinistra)

k = costante elastica, che indica la rigidità della molla

- = la forza elastica è una forza di richiamo, diretta sempre verso l’equilibrio

ux = è il versore dell'asse x (da la direzione)

Il meno o anche chiamato Richiamo identifica la forza elastica come una forza di richiamo cioè che tende a riportare la molla nella lunghezza di riposo.

Facciamo degli esempi per comprendere meglio il concetto di Forza Elastica.

Allungamento:

Se il nostro sistema di riferimento è verso destra la forza elastica sarà opposta. I valori sulla x nel nostro caso è positiva essendo il sistema verso destra. Essendo la x positiva la la F (Forza) essendoci il meno del richiamo allora sarà negativa perché 

- ∙ + = - (meno per più è uguale a meno).

Compressione:

Se invece la x è negativa, allora la molla viene spinta verso sinistra e la forza elastica va verso destra visto che deve tornare nella posizione di equilibrio. Essedo la x negativa la F (Forza) essendoci il meno del richiamo allora sarà positiva perché

- ∙ - = + (meno per meno è uguale a più).

In sintesi:

• x positivo → allungamento → forza negativa

• x negativo → compressione → forza positiva

La costante elastica k descrive la rigidità: più k è grande, più forza serve per deformare la molla.

MOTO DI UN CORPO COLLEGATO AD UNA MOLLA:

Ora analizziamo il moto di un corpo collegato ad una molla. Il moto riprende le leggi che abbiamo studiato nel moto armonico e viene chiamato oscillatore armonico.

Con oscillatore armonico si intende:

Un corpo sul quale agisce una forza proporzionale allo spostamento e di verso opposto.

La molla ne è l'esempio perfetto.

Spostando la molla essa ha ottenuto una velocità e per inerzia continuerà a muoversi fino a che non ritorna nella posizione di equilibrio o riposo. Infatti ciò che abbiamo descritto sopra è ciò che mancava nella spiegazione di prima.

diamo per scontato non parlando di cosa accade nel tratto in cui il corpo viene mosso fino a che il corpo ritorna a riposo. Se non ci fosse l'attrito la molla continuerebbe a "rimbalzare"(oscillare) all'infinito.

Ora entriamo nel vivo dell'argomento.

Il moto risultante per effetto di una forza elastica è rettilineo qualora la velocità sia nulla o diretta verso il versore ux.

Calcoliamoci l'accelerazione:

Prendiamo la formula della Legge di Hooke (nei calcoli il versone ux non si scrive)

F = - k ∙ x

grazie alla seconda legge di Newton

F = m ∙ a

quindi

F = - k ∙ x =  m ∙ a

allora con la formula inversa se vogliamo calcolarci l'accelerazione otteniamo:

a = - k/m ∙ x

Ma se a = - k/m ∙ x

e

F = - k ∙ x

allora possiamo dire che

a = F / m

Nel moto armonico abbiamo trovato questa relazione.

Dunque una molla si muove di moto armonico.

Riprendendo a = - k/m ∙ x e ponendo ω^2 = k /m  si ottiene a = - ω^2 ∙ x

Dunque l'accelerazione è direttamente proporzionale allo spostamento ed è massima quando il corpo si trova agli estremi di oscillazione. L'accelerazione invece si annulla nell'origine dell'oscillazione (punto di equilibrio).

Nel moto armonico

ω = 2π / T.

Calcoliamoci il periodo che è

Il periodo è l'intervallo di tempo necessario affinché il corpo iniziando da una posizione ritorni alla stessa posizione dopo aver compiuto una oscillazione completa.

Ora però se cerchiamo di arrivare a scrivere l'equazione dell'oscillatore armonico arriviamo a scrivere una equazione differenziale. Chi fa fisica 1 di solito sta facendo al massimo in parallelo Analisi 1. Essendo spiegate le equazioni differenziali in Analisi 2 ed essendo molto lunga la spiegazione ho deciso di scrivervi le varie formule che si possono ricavare.

Nel capitolo delle oscillazioni approfondiremo bene quindi non è un addio ma un arrivederci.

Equazione differenziale del moto armonico semplice:

Pulsazione:

Legge oraria:

Periodo:

La forza elastica e il moto di una molla rappresentano un perfetto esempio di moto armonico semplice, uno dei fenomeni più importanti della fisica classica. Attraverso la Legge di Hooke, possiamo descrivere in modo preciso come una molla reagisce a una deformazione, mentre lo studio dell’oscillatore armonico apre la strada alla comprensione di sistemi molto più complessi, dalle vibrazioni meccaniche alle onde sonore.

Buono studio!